top of page
Assíntotas Verticais e Horizontais

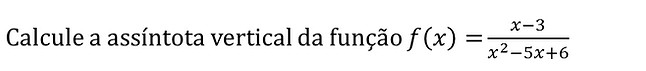


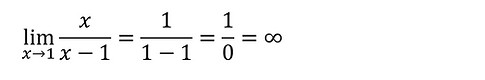
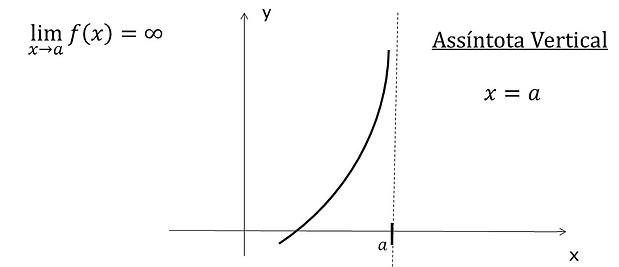
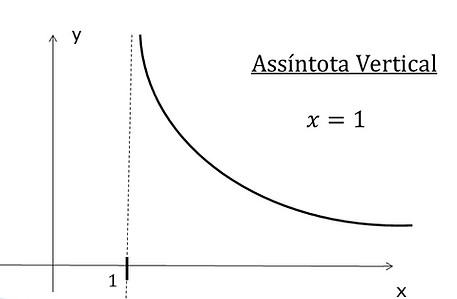

Quando x tende a "a" e a função f(x) tende ao infinito temos uma assíntota vertical x = a. Veja no gráfico a seguir:
Assíntotas Verticais
Vejamos um exemplo numérico:
Agora vamos calcular uma assíntota:
Para obter um limite no infinito o denominador tem que ser zero. Qual valor atribuímos para x para que o denominador seja zero? Para isso basta igualar o denominador a zero e resolver a equação:
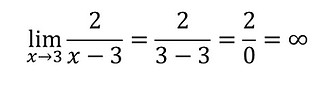
Ao substituir o x por 3 temos um limite tendendo ao infinito.

Vamos a mais um exemplo:
Agora preste bastante atenção no exemplo a seguir:
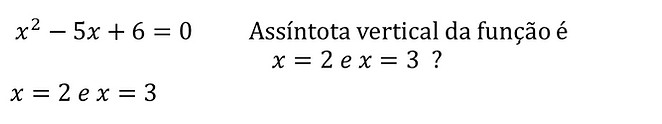
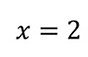
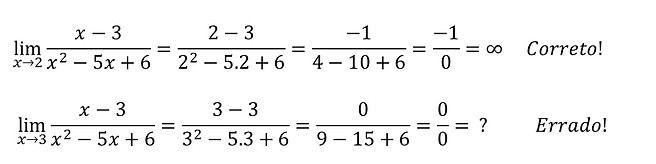
Vamos testar os resultados para verificar se o limite tende ao infinito:
Como podemos ver para x = 3 não temos infinito, temos indeterminado, ou seja, o valor atribuido para x deve zerar o denominador mas não deve zerar o numerador, por tanto a resposta será:
Assíntota vertical da função é
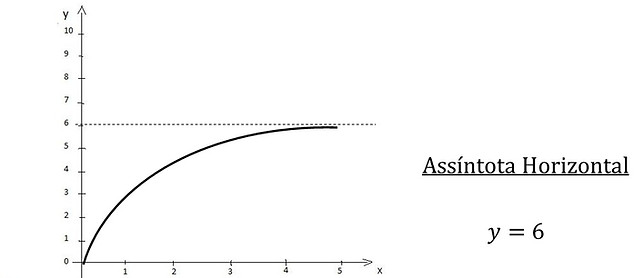
Assíntotas Horizontais
Quando x tende ao infinito e a função f(x) tende a um valor real "a" temos uma assíntota horizontal y = a. Veja no gráfico a seguir:
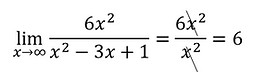
Vamos calcular uma assíntota horizontal:


Para efetuar esse cálculo basta colocar a função em um limite com x tendendo ao infinito, veja:
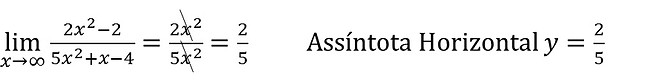
Vamos a mais um exemplo:
Só existe assíntota horizontal se a função tender para um número real, se a função tender para o infinito a função não admite assíntota horizontal.
Exercícios resolvidos na vídeo-aula:
bottom of page

