top of page
Limites com Raízes
Determinados e Indeterminados
Para efetuar o cálculo de limites com raízes o procedimento é o mesmo, basta substituir x pelo valor ao qual ele esta tendendo. Vamos ver alguns exemplos:
Limites com Raízes - Determinados e Indeterminados
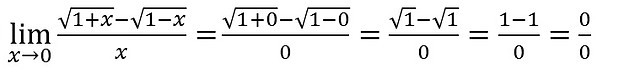

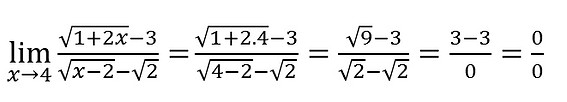
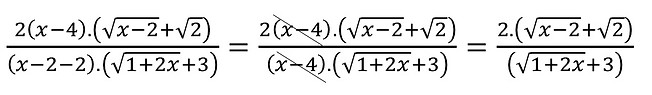
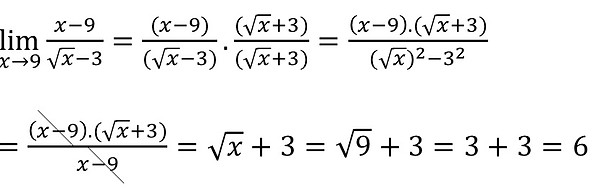
Para fugir dessa indeterminação vamos multiplicar tanto o numerador quanto o denominador pelo conjugado do denominador e efetuar os cálculos. Assim temos:
Vamos a mais um exemplo:

Para fugir dessa indeterminação vamos multiplicar tanto o numerador quanto o denominador pelo conjugado do numerador e efetuar os cálculos. Assim temos:
Vamos ao nosso último exemplo:
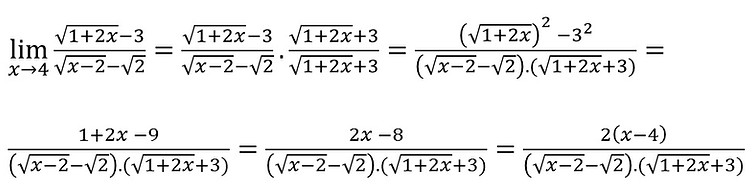
Como temos raízes tanto no numerador como no denominador vamos ter que racionalizar os dois, vamos começar multiplicando tanto o numerador quanto o denominador pelo conjugado do numerador e efetuar os cálculos. Assim temos:
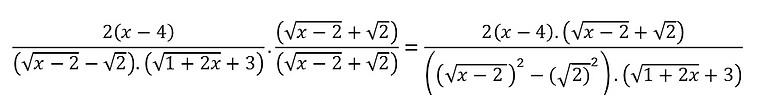
Agora que já conseguimos racionalizar o numerador, vamos multiplicando tanto o numerador quanto o denominador pelo conjugado do denominador e efetuar os cálculos. Assim temos:
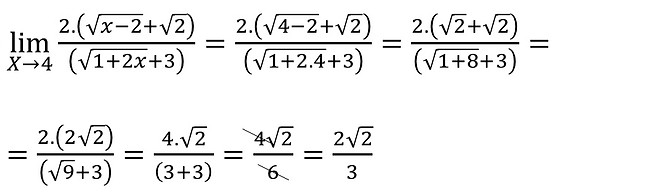
Agora que temos uma função simplificada vamos substituir o valor de x por 4 e efetuar os cálculos:
Encontrando assim o resultado real do limite.
Para mais detalhes acesse a vídeo-aula:
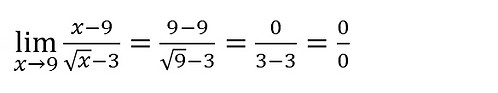
bottom of page

