top of page
Dispositivo Prático de Briot-Ruffini no Cálculo de Limites
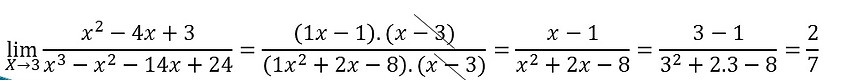

Dispositivo Prático de Briot-Ruffini no Cálculo de Limites
Para resolver o limite da função f(x) quando x tende a "a" basta calcular f(a), ou seja, basta substituir x pelo número "a", assim temos:
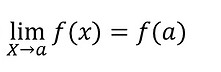
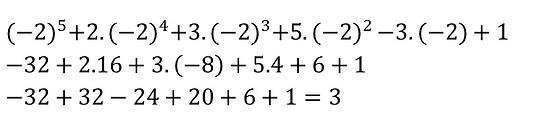
Vamos a um exemplo:
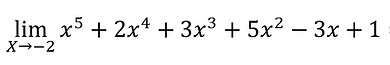
Foi preciso efetuar vários cálculos para obter o resultado do limite. Agora, o que acontece se os cálculos forem efetuados através do Dispositivo de Briot-Ruffini? Vamos ver:
Observe que o último valor obtido pelo dispositivo é exatamente o valor do limite da função e isso não é coincidência. Sempre que efetuamos os cálculos com o dispositivo, o ultimo número será sempre o resultado do limite da função, e isso é incrível!
Vamos para mais um exemplo:
Não vamos utilizar o método tradicional, vamos efetuar os cálculos direto pelo Dispositivo Prático de Briot-Ruffini. Como temos dois polinômios teremos dois dispositivos.
Resultado para o polinômio de cima (numerador)
Resultado para o polinômio de baixo (denominador)

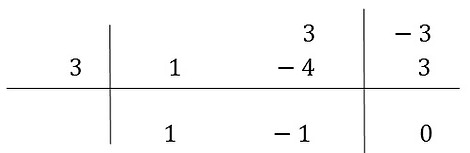
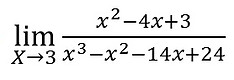
Como podemos ver o resultado do limite é indeterminado.

Como sabemos toda vez que encontramos um resultado indeterminado basta fatorar os polinômios e o Dispositivo de Briot-Ruffini já nos dá os coeficientes do polinômio fatorado, ou seja, ao utilizar o Dispositivo de Briot-Fuffini efetuamos dois passos em um só! Vamos escrever os polinômios de forma fatorada e efetuar os cálculos.
Para mais detalhes acesse a vídeo-aula:
Para o cálculo de limites de funções polinomiais esse é o método mais prático.
bottom of page

