top of page
Introdução aos Limites e Limites Laterais
Introdução aos Limites e Limites Laterais
Temos a função f(x) representada no gráfico a seguir. Quando x tende a "a" pela esquerda, ou seja, por números menores do que "a", a função f(x) se aproxima cada vez mais de L1, assim sendo, podemos dizer que o limite da função f(x) quando x tende a "a" pela esquerda é L1.


Quando x tende a "a" pela direita, ou seja, por números maiores do que "a", a função f(x) se aproxima cada vez mais de L1, assim sendo, podemos dizer que o limite da função f(x) quando x tende a "a" pela direita é L1.
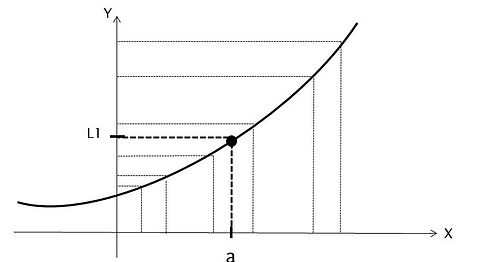

Podemos observar que tanto pela esquerda quanto pela direita os limites laterais são iguais, assim sendo podemos dizer que o limite existe quando x tende a "a" e não precisamos especificar por qual lado estamos nos aproximando. Em simbologia matemática temos:
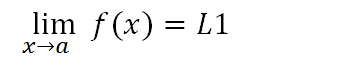
Temos a função f(x) representada no gráfico a seguir, quando x tende a "a" pela esquerda, ou seja, por números menores do que "a", a função f(x) se aproxima cada vez mais de L1, assim sendo, podemos dizer que o limite da função f(x) quando x tende a "a" pela esquerda é L1.


Quando x tende a "a" pela direita, ou seja, por números maiores do que "a", a função f(x) se aproxima cada vez mais de L2, assim sendo, podemos dizer que o limite da função f(x) quando x tende a "a" pela direita é L2.
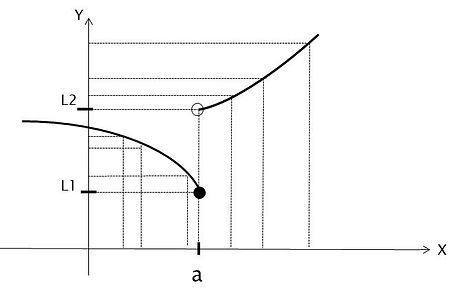

Podemos observar que o limite lateral esquerdo é diferente do limite lateral direito, assim sendo dizemos que o limite da função f(x) quando x tende a "a" não existe. O que existem são seus limites laterais esquerdo e direito.
Atividades resolvidas na vídeo-aula:
bottom of page

